ShapFuzz:论文阅读

SHAPFUZZ: Efficient Fuzzing via Shapley-Guided Byte Selection

Abstract

​ 基于变异的模糊测试是一种流行且有效的技术，用于发现程序中的漏洞和未覆盖代码。然而，只有少数研究关注量化输入字节的重要性。每个输入字节的重要性由其在发现新代码中的贡献程度决定。以前的工作往往集中于获取输入字节与路径约束之间的关系，而忽略了并非所有与约束相关的字节都能发现新代码的事实。在本文中，作者进行Shapley分析来理解字节位置对模糊测试性能的影响，发现某些字节位置比其他字节位置贡献更大，并且这种特性通常在不同的种子之间保持一致。基于此观察结果，我们提出了一种新颖的解决方案，成为SHAPFUZZ，以指导模糊测试过程中的字节选择变异。具体而言SHAPFUZZ在模糊测试期间每次测试输入时，以低开销更新字节的Shapley值（重要性）。它利用上下文多臂老虎机（CMAB）算法在变异高Shapley值字节和和低频选择字节之间进行权衡。作者基于AFL ++实现该解决方案的原型，即SHAPFUZZ，并针对包括五个字节调度Fuzzer和五个常用的Fuzzer在内的十个最先进的模糊器对其进行评估。与字节调度模糊器相比，SHAPFUZZ发现了更多边。它还在三组不同的初始种子集上暴露了比最佳基线更多的漏洞。SHAPFUZZ比最佳常用的模糊器多暴露20个漏洞，并且在MAGMA上比基线多发现6个CVE。此外，SHAPFUZZ在6个广泛使用的程序的最新版本上发现了11个新漏洞，其中3个漏洞已得到供应商的确认。

Introduction

基于变异的模糊测试，核心是：**变异哪些字节？**这些字节该用什么值？

作者将Shapley值法应用于模糊测试的havoc变异阶段，指导应当变异哪些字节组合。

在确定变异字节的方向中，先前已有的研究：

  • TaintScope/Dowser/Angora依赖于额外的分析(污点分析)来识别与路径约束相关的字节
  • GREYONE/REDQUEEN/ProFuzzer/PATA间接推断字节和约束之间的依赖关系
  • NEUZZ/MTFuzz/EMS从历史数据中提取信息来找到变异的位置

现有研究不足之处

  • 前文所提及的解决方案中平等地对待所有与约束相关的字节，在无法发现新代码的字节上浪费时间和能量。
  • 现有的解决方案所需的额外分析阶段通常由于其逐字节调查而非常耗时，代价较高。
  • 对于基于深度学习的Fuzzer，这个额外的分析阶段甚至可能导致模糊测试过程失败，因为构建模型时，输入尺寸过大会导致内存不足。

解决方案

​ 作者的关键思路是量化与约束相关字节的重要性，而不需要额外的分析阶段。新区域的发现是由于某些字节的合作，准确来说是它们协作变异的结果。作者从合作博弈论的角度出发，将模糊测试的字节调度部分视为Shapley Analysis的“过程”。

过程：作者在Fuzzing中应用Shapley分析，通过计算字节组合中每个字节的边际贡献

​ Shapley Analysis被广泛用于量化每个参与者对结果的贡献。通过量化输入字节的重要性，可以找到更有可能发现新代码的字节，并在这些字节上进行更多的变异尝试。Shapley Analysis可以集成到变异过程中，因此不需要额外的分析阶段来获得字节的重要性。

Shapley Analysis

​ 在合作博弈论中，玩家联盟共同参与游戏并获得收益。关键问题是每个玩家对联盟的贡献程度。为了解决这个问题，人们提出了许多方法。其中最著名的解决方案是Shapley值，这是一种在合作博弈中分配收益的方法。具体来说，Shapley值是每个玩家对所有可能的玩家联盟的边际贡献的加权平均值。此外，Shapley值已应用于许多领域，例如量化深度学习模型中特征的重要性。简单来说，就是一个由玩家组成的联盟参加一场游戏获得收益，那么如何分配收益才是公平的？Shapley值用来解决这个公平分配问题。

​ 本文的核心在于Shapley值法的应用。重要的就是计算每个玩家的边际贡献。如图，举例说明：

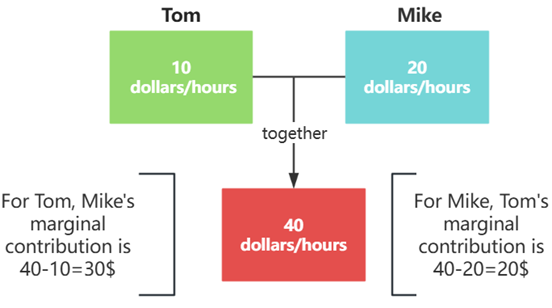
​ 现在假设Tom每小时能挣10美元，Mike每小时能挣20美元，他们一起作为一个联盟每小时能挣40美元。那么现在便有个问题，该如何分配这40美元？平均分配显然对Mike来说不公平。通过Shapley值法，先计算各自的边际贡献。A的边际贡献即是A给联盟其他人带来的价值。那么对Tom来说，Mike的边际贡献就是40-10=30。对Mike来说，Tom的边际贡献就是40-20=20。根据Shapley值法，Tom应该获得的收益为(10+20)/2 = 15$，Mike应该获得的收益为(20+30)/2=25$。

​ 在模糊测试中的变异阶段，fuzzer会将选择好的种子进行变异，fuzzer的变异算子会改变某个随机字节或比特位的值（例如，位翻转，字节算术加减随机数等）。变异代价相对执行而言小很多，因此通常对一个种子变异多次，这会形成该次变异的字节组合。具体而言，作者将一次变异中值发生改变的字节作为一个字节组合。将每个字节组合作为一个联盟，每个字节作为一个玩家，发现新区域（新边）的数量作为收益R，来计算每个字节的临时Shapley值以指导下一次变异该选择哪些字节进行变异。

Motivation

​ 由于字节是协同变异以探索代码的，因此作者使用Shapley值的方法来分析字节的贡献。作者首先通过以下两个观察实验来确定字节具有不同的重要性

Experiment of Shapley Analysis

​ 为了计算种子中字节的Shapley Value, 作者将一个组合发现的新边数量视为收益。然而，一个长度为N的种子有256^N种可能的组合，数量过多无法进行测试。为获得字节的相对准确的Shapley Value，作者对单个种子进行48小时的随机变异模糊测试。

  • 观察实验一：

    • 使用AFL++对18个程序进行模糊测试。一个程序的corpus只存在一个种子，且不更新种子队列。即持续地变异（移除改变种子长度的变异器）所选的初始种子。重复实验六次。

    • 期间，执行恢复策略。即{1,3,4}字节组合发现新边收益为R0，那么将执行其所有子集，得到收益R1~Rn，共同计算各个字节的Shapley值。（为了与Shapley值法的定义保持一致）

    • 实验结果如下：

      image-20240918153959734

      每个点表示对于一个程序和一个初始种子，前 X% 的字节贡献了 Y% 的新边。由实验结果可知，一小部分字节对发现新边的贡献最大。

  • 观察实验二：

    • 使用GreyOne的FTI方法分析16个程序中CMP之间相关字节的重叠情况。即，给定一个CMP和种子，如果改变种子的第i个字节会导致CMP j的值发生改变，那么字节i与CMP j相关。实验结果如下图所示：

    • image-20240918154941625

      大多数字节与多个CMP指令相关。这个实验表明，CMP之间相关字节的共享是一种普遍现象。换句话说，少部分字节与多个路径约束相关。

​ 通过观察实验，作者发现，只有少部分字节对探索新区域贡献最大，因此可以利用Shapley分析来获取这些高重要性字节，并在模糊测试期间分配更多能量给它们。由于与约束相关的字节通常与多个CMP指令相关，因此专注于高重要性字节可以提高在未见路径中发现代码的效率。

Design

​ SHAPFUZZ专注于字节变异，量化字节位置的重要性。将相同长度的种子理解为一个Shapley分析过程。即，从同一个原始种子保留下来且不改变长度的种子属于同一个合作博弈，并且共享相同的字节Shapley Value。为了将Shapley Analysis融入到Fuzzing中，作者提出以下设计方案。

image-20240918155507735

  • Shapley Analysis Among Bytes

    Shapley Analysis，前文提过。指玩家联盟共同参与游戏并获得收益，假设联盟S在游戏中获得的收益为R，根据每个玩家的贡献程度来分配收益。Shapley值法能够量化每个玩家的贡献程度，因此合理分配联盟收益。

    • 一个长度为N的种子，有N个字节。将每个字节作为玩家，即有N个玩家。一次完整的Shapley分析会将2^N种组合的收益都计算得出。每一个字节组合（一次变异中的所有发生变化的字节组成）都作为一个联盟。每一个联盟的收益都会被算出。放在模糊测试中，每一个字节组合{x_1,x_2,…,x_i}都应该被变异执行一次，以获得收益（发现新边的数量）。

  • Shapley Analysis In One Seed

    • 如果收益定为一次Fuzzing结束后新发现边的数量，由于新发现的边是通过与当前覆盖状态进行比较获得的，那么同样的字节组合在不同的时间执行相同的变异发现新边的数量是不同的。举例来说，在Fuzzing初期字节组合{1,3,4}变异并执行结束后会得到一个位图，与全局位图进行比较以确定是否发现新边。随着Fuzzing的进行，全局位图在不同时间有不同状态，所以在另一时间该字节组合以相同变异并执行得到的位图虽然没有变化，但是全局位图发生了变化，相比较所得到的新边数量就会发生变化。

    ​ 因此，作者将收益R定义为自新边(self-new edges)的数量，作者定义自新边为将输入i发现的边与初始种子S0发现的边进行比较时发现的新边。也就是说，每个组合变异执行得到的位图不与全局位图进行比较，而是与初始种子的位图进行比较。

  • Shapley Analysis Across Seeds

    从Shapley分析的角度看，多个种子可以被视为一个种子。如果变异没有改变原始种子S0的长度，该变异得到的新种子S1实际上就是种子S0的Shapley分析的一个组合。因此，可以将长度相同的种子视作一个家族(family)。那么”family”会有以下特征：

    • 家族中所有种子都由初始种子变异而来
    • 所有种子具有相同的长度。
    • 每个种子的字节位置一致，因此每个字节Shapley值在每个种子中是一致的

    执行Shapley Analysis的过程会产生新的种子，如果新种子长度没有变化，那么其实际上就是原始种子Shapley Analysisi的一个字节组合。如果长度发生变化，则字节的相对位置，以及Shapley Analysis中的玩家数量发生了变化。针对于Fuzzing过程中长度发生变化的种子，作者采取以下措施：

    • 针对于改变长度的变异操作，将这些操作存储至M1中。
      • 若改变长度的种子未发现“新边”（not self-new edges），那么不保存，抛弃即可。（遵循遗传算法）
      • 若改变长度的种子发现了“新边”，则利用M1撤销长度变异操作。再次执行。
        • 倘若能够发现相同的“新边”，那么则将撤销长度变异操作后的新种子加入其初始种子的family中。
        • 倘若不能够发现相同的“新边”，那么将改变长度的新种子作为初始种子加入一个新的family

    该过程如下图所示：

    image-20240918155413346

​ Shapley值的更新可以嵌入到Fuzzing的变异阶段。变异产生的未改变长度的测试实例都是一个Shapley分析中的字节组合。该测试实例执行后，都可以根据执行结果计算收益R。利用这个收益R更新字节的Shapley值。但是更新期间，应该只针对与约束条件相关的字节。换句话说，只更新与约束条件相关字节的Shapley值。那么，在某次字节变异组合{1,3,4}执行后发现了自新边。需要精简该字节变异组合，筛选出其中的必要字节。即，分别执行{1,3},{1,4},{3,4}。倘若{1,3}的执行结果与{1,3,4}的结果相同，那么字节{4}便是冗余字节。此次Shapley值更新将排除字节{4}。

​ 更新过程中，需要计算每个字节Shapley值，也就是每个字节对字节组合的边际贡献。根据Shapley值法的计算方式，需要获得所有子集的收益R，上述例子中必要字节组合{1,3}的值更新过程中，会执行{1},{3}获得其收益R1和R3以计算字节{1},{3}对联盟{1,3}的边际贡献。

在代码实现中，字节的Shapley值=自新边数量/必要字节数量。且每个必要字节的Shapley值相同。（如果严格按照Shapley值法定义来计算，在Fuzzing期间应该恢复字节组合的子集并执行。这样效率就过低，且计算出的Shapley值仍然是一个不完整的。）

​ 随着Fuzzing的进行，每个家族的字节Shapley值会不断更新。仅根据当前计算得到的字节Shapley值来选取需要变异的字节是不够的，因为，Shapley值的计算仅基于输入空间的一部分得到，它不能保证具有高Shapley值的字节总是保持高值。所以，当Fuzzing过程中，一些字节因为高Shapley值被频繁选中但未发现新边时，便不能在这些字节上浪费更多能量。所以需要在高Shapley值和低频选择字节之间平衡。

  • Shapley-guided Byte Selection

    ShapFuzz使用上下文多臂老虎机（CMAB）来实现Shapley值的权衡。而作者所采取的求解算法为最大置信区间上界算法（Upper Confidence Bound），置信区间是概率统计和统计推断比较重要的概念，其衡量一个随机变量分布的置信水平。置信区间越大，越说明这个随机变量不确定因素更大。UCB则是采用置信水平来实现对Exploitation和Exploration之间的平衡。

    利用Shapley值，为字节选择构建概率分布，即CMAB为每个字节计算分数。分数越高的字节被选择的概率越高。

    • $$Score(s,p)=E[r_{s,p}|f_S]+0.5U_{s,p}+\phi_p$$

      • 其中r_{s,p}是该输入所执行路径的稀有性。

    • 在代码中实现的方案

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      // before havoc mutation stage.
      // centers had been generated.
      for(u32 i = 0;i < afl->centers_num;i++){
          // distance: between ancestor seed path and every center path.
        double distance = (double)cal_distance(cur, afl->centers[i], map_size);
          // input->feature_vec->data is the cosine similarity of every center. 
        afl->queue_cur->feature_vec->data[i] = distance;
      }
      // every_score:  one byte of mutation.
      every_score = r1->data[0] + m3 + ancestor_node->mutated_pos[ii].SV;
      // ...
      score = sum(every_score);
      // generate a random number between 0 and score.
      double choose = ((double)rand()/RAND_MAX) * score;
      // history_mutation_sequence_idx is the quantity of mutations bytes 
      for(u32 i = 0;i < afl->history_mutation_sequence_idx;i++){
          // find first byte greater than choose  
          if(afl->distribution[i] >= choose){
              return afl->history_mutation_sequence[i];
      	}
      }
      // else return random one position

      对every_score作如下说明：

      $$r_1 = (A^{-1}\times b)^T \times f_s，m_3 = 0.5 \times \sqrt{f_s^T \times A^{-1} \times f_s}，SV=Shapley Value.$$

      f_s存储于feature_vec中。A被初始化为k × k，对角线全为1的矩阵。b被初始化为k × 1，全为0的矩阵。其中A矩阵的更新方式为$$A = A.data+ f_s × f_s^T$$。B矩阵的更新方式为$$b = b.data+ R × f_s$$,其中R为收益。

作者提出的一些局限性：

  • Shapley值计算的开销：Shapley将字节变异的过程建模为一个合作博弈，并使用Shapley分析来量化每个字节的贡献。假设在一个变异中发现了自新边，并且其变异位置的数量为N。为了计算Shapley值，我们需要分析在$$2^N$$个变异位置子集中发现的自新边数量。为了降低开销，SHAPFUZZ使用两种特殊情况来简化Shapley分析过程。首先，如果存在不影响自新边结果的冗余字节，我们移除这些字节以减少N。其次，如果变异字节是发现自新边所必须的，那么这些字节具有相同的Shapley值。然而，如果这两个条件都不满足并且N很大，就会引入一些开销。将来，我们可以使用轻量级和改进的Shapley分析算法来缓解这个问题。
  • 可变种子长度：此外，SHAPFUZZ建立了一个族系系统来减轻Shapley分析带来的开销。在一个族系中，同一族系的种子对于字节具有相同的Shapley值。然而，在维护族系时，我们忽略了改变长度的变异输入。这是因为使用改变种子长度的变异器可能会扰乱种子种的字节位置，我们无法实现种子间的位置映射。将来，我们可以研究可变长度Shapley分析的数学理论。在现有版本中，如果通过改变长度生成一个新的种子，我们将使用这个种子创建一个族系来缓解这个问题。
  • 自新边影响：随着时间的推移，新边发现变得越来越困难，SHAPFUZZ 利用自新边作为衡量收益和识别可能影响多个分支的字节的指标。然而，在某些情况下，导致自新边的字节并不一定会导致发现额外的新的边。这些自新边可能已经被其他种子发现。因此，具有高沙普利值的字节实际上可能比沙普利值所指示的贡献更少。如果我们为这些字节分配了过多的能量，会导致模糊效率下降。例如，假设种子中的字节 i 与 y 条边相关联。如果所有这 y 条边都被探索过，我们可以推断字节 i 已经做出了重大贡献。然而，由于与字节 i 相关的所有边都被探索过，为字节 i 分配任何能量都不会帮助发现新的边。
  • 族系内部语义一致性：为了减少计算沙普利值的开销，同一个族系中的种子共享相同的Shapley值。然而，尽管实施了严格的族系构建方法（具有遗传关系和相同长度的种子），但仍然可能存在种子之间语义不一致的情况。语义不一致会导致具有不同含义的字节共享相同的沙普利值，从而错误地估计字节的重要性。例如，**长度字段通常可以决定后续字节的语义。在这种情况下，我们的方法无法保证种子之间的语义一致性。**假设存在一个种子 A，其中字节 i 是一个长度字段。种子 B 是通过变异字节 i 从种子 A 派生出来的。由于长度字段的改变直接改变了后续字节的含义，因此字节 j（紧随字节 i，位于种子 A 和种子 B 中的相同位置）很可能具有不同的含义。这意味着即使种子 A 和种子 B 具有相同的长度和遗传关系，种子 A 和种子 B 中的字节 j 在语义上也不一致。如果我们继续在这两个种子中共享字节 j 的沙普利值，就会导致Shapley值不准确，使一些低效的字节被分配到更高的变异能量，从而影响模糊效率。

Questions&Ideas

  • 以自新边为收益R，但是代码中的原始种子的virgin_bits会改变。那这跟文章中自新边的定义便冲突了。同一变异还是会获得不同收益。
  • Shapley值计算方式效率很高，但可能指导价值就不够大。
    • 每个字节的Shapley值更新方式: self-new edges / necessary bytes
    • 并且，每一次变异执行后都会累加。那么字节的Shapley值实质就是，这个字节从Fuzzing开始至现在发现自新边的能力。而自新边的定义在代码中又被修改成”family”中全局的virgin_bits。**那么针对同一个”family”而言，就是给历史发现“新边”数量越多的字节分配更多的能量。**再根据多臂老虎机，在能量低次数少与能量高次数高的字节间平衡。所以，这个Shapley值法的应用，笔者认为是作者为了发论文所附加上的，代码也应可以简化。
  • 以下是笔者一些ideas，当然建立于Shapley值能够很好应用于Fuzzing的前提下。
    • 针对文章提出的语义一致性问题，可以使用Pit文件来指导变异。针对一些会改变种子语义的字段变异，便不适用Shapley值或使用一个较低的值。等待CMAB选中这些特殊语义字段时，再决定如何变异。（参考Peach fuzzer）
    • 可以尝试在AFL++上实现一个基于字节历史表现来分配变异能量,并利用CMAB来平衡低次数字节与高次数字节的策略。并看看和SHAPFUZZ的效率差异。
Paper
#Paper
ShapFuzz:论文阅读
https://loboq1ng.github.io/2024/08/07/ShapFuzz：论文阅读/
作者
Lobo Q1ng
发布于
2024年8月7日
许可协议